Selected notes for talks

For a list of all my academic talks, see my CV. See also the Expository Notes page for a lot of my other mathematical writing.

Before giving a talk, I usually make an electronic handwritten version of my notes -- I am making a selection of these notes, which may be of general interest, available.

• Notes for a Journées Arithmetiques talk on local systems of geometric origin.

• Here’s a 12 minute video about some of my recent work on finiteness of monodromy representations, from a short talk I gave at the IAS. Here is a longer talk on the same subject, which I gave at IPAM.

• Arithmetic restrictions on geometric monodromy -- notes from a talk about my recent work on fundamental groups and geometric monodromy, at Oberwolfach.

• Non-abelian Lefschetz hyperplane theorems -- notes from a talk on my thesis work and some applications. I've given many versions of this talk; this particular set of notes was from a talk at Stony Brook. If you've seen another version of this talk and are looking for something not in this particular set of notes, let me know.

• Dynamical Mordell-Lang and automorphisms of blowups -- notes from a talk I gave at Princeton on joint work with John Lesieutre. Again, I've given several talks on this topic; this is one representative set of notes.

For general audiences

Every once in a while, I'll give a talk to high school students or undergraduates (and once or twice to more general audiences).  Below are some notes and slides from such talks.

• Graphs and representation theory -- a talk using Lie algebra representation theory to prove some facts from graph theory. The talk is aimed at undergraduate math majors.

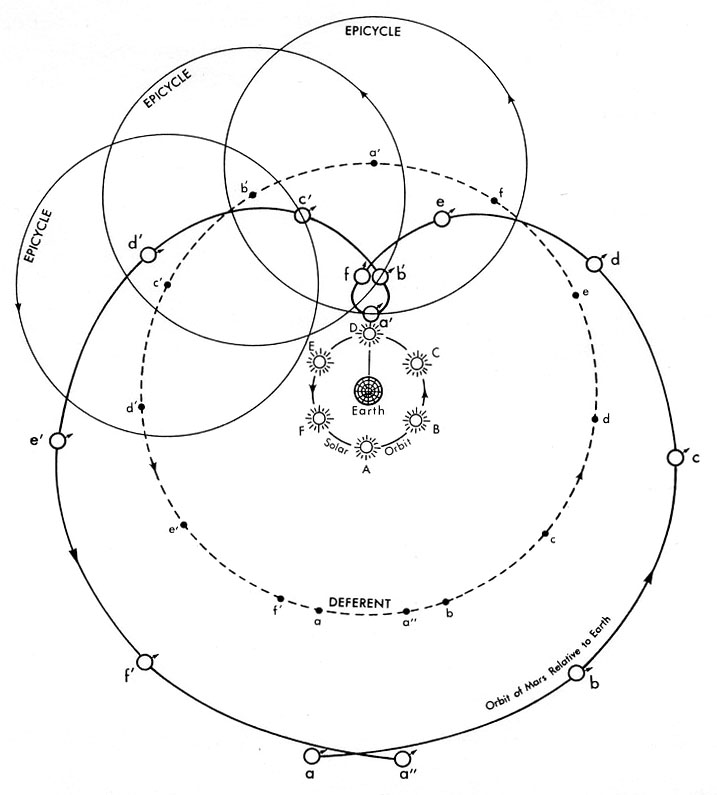
• The music of the spheres -- a talk about the history of (mostly incorrect) theories of cosmology, from Pythagoras to Kepler. Largely inspired by Arthur Koestler's The Sleepwalkers.

• Tiling problems -- a talk about tiling problems (feasibility, counting, etc.) aimed at an undergraduate audience.

• Zeroes of integer linear linear recurrences -- a talk about the Mahler-Skolem-Lech theorem, characterizing the possible zero sets of integer linear recurrences; includes a baby introduction to p-adic analysis. The talk is aimed at undergraduate math majors.

Selected Older notes

Here are some old notes which might be useful.

• Motivic analytic number theory -- a talk about some of my work on the Grothendieck ring of varieties.

• The cotangent complex -- expository notes from a talk on the cotangent complex from a seminar at Stanford about perfectoid spaces.

• The fundamental group and polylogarithms -- notes from an expository talk at Columbia, about Deligne's paper on the fundamental group of the projective line with three points removed.

• The pairing on the Brauer group -- notes from an expository talk on the pairing on the l-power torsion in the Brauer group of a surface over a finite field, following Tate. The talk was for a seminar at Columbia.

Miscellaneous

Here are some notes to myself about things I thought about a while ago, and notes other people have taken on casual talks I've given.

• Homotopical enhancements of cycle class maps -- at some point I thought about enhancing the cycle class maps to intermediate Jacobians to fancier gadgets (maps to higher analytic stacks). I think there are some intriguing heuristics that suggest such constructions might be useful, but I was never able to make anything work. These notes are not written in a rigorous way, so let me know if you have questions about how to make things rigorous.

• Sam Nolen took some notes on two talks I gave a while ago: Here are notes on a talk I gave on some ideas related to Verdier duality and scanning in algebraic topology (the document also contains notes on a nice talk by Arnav Tripathy). And here are some notes on a talk I gave about "motivic analytic number theory" on a decommissioned icebreaker in the San Francisco bay (the document also contains notes on a nice talk by Jeremy Booher on the Weil conjectures and on Serre's Kahler analogue thereof).