An NSERC Proposal

I try to make a habit of posting my grant proposals here after the application period has passed, both because I hope people might find them to be useful models, and because doing so is a good opportunity for a brief postmortem.

If you’d like to take a look at my proposal for the NSERC Discovery grant, you can do so here. The proposal was funded, so hopefully it is a reasonably good model.

The NSERC format has the benefit that it is somewhat brief, so writing the proposal is reasonably low-effort; this has the side-effect, unfortunately, that the proposals cannot be very detailed (or readable).

On reading the proposal, I am a bit struck at how quickly many of the projects therein were completed; many of them are already done and on the arXiv! Of course a few of the more ambitious projects mentioned are still far from complete. On the other hand, it’s interesting to see how some of my current interests have already diverged a bit from the proposal — for example, I’m now thinking quite a bit about the p-curvature conjecture, but the approach I have in mind is somewhat different than what I had proposed at the time.

And I think my output in the last year or so has (maybe unusually and perhaps immodestly) been quite a bit more interesting than what was proposed. In particular this paper proves something I’d wanted to prove since I was a postdoc, and there’s very little hint of it in the proposal.

Tiling puzzle: solution

My last post was a little tiling puzzle: you can read it here. In this post I want to quickly give the solution.

Represent a red tile by \(1\) and a blue tile by \(-1\); and think of the square in coordinate \((a,b)\) as the monomial \(x^ay^b\). Then the question is equivalent to asking when the polynomial \(p_{N,M}(x,y)=\sum_{a=1}^N\sum_{b=1}^Mx^ay^b\) is in the ideal generated by \((1-x+x^2, 1-y+y^2)\). These are cyclotomic polynomials for sixth roots of unity, so one can test whether \(p_{N,M}(x,y)\) is in this ideal by evaluating it at \((\zeta, \zeta)\), where \(\zeta\) is a primitive sixth root of unity. Now it’s an exercise to check that \(p_{N,M}(\zeta, \zeta)=0\) if and only if one of \(N,M\) is divisible by 6!

A tiling puzzle

Here are four magic triominoes:

Four magic triominoes

Each is made out of three squares, two red and one blue or two blue and one red, alternating in color. These squares have the following property: if you place two squares of the same color on top of each other, they stack. On the other hand, if you place a red square on top of a blue square, they annihilate each other.

For example, if you place the following two triominoes, so that the rightmost square of the first aligns with the bottom square of the second, you get the following configuration:

Placing two triominoes so that squares of opposite colors are on top of each other annihilates those squares.

But if you place the same two triominoes so that the middle square of the first aligns with the bottom square of the second, those two red squares stack, which I’ve indicated by a two below (i.e. there is a stack of height two at that location):

Your goal is: given an N x M chessboard of squares, place these triominoes onto the chessboard so that every square is covered by exactly one red tile. (Note that the tiles aren’t allowed to stick off the edge of the board.)

For which (N,M) is this possible (with proof)? Feel free to post solutions in comments; if no one posts a solution in a week or so I’ll update with a solution.

Tensor powers of faithful representations

Let \(G\) be a finite group and $$\rho: G\to GL_r(V)$$ a faithful representation, with \(V\) a finite-dimensional complex vector space. The following is well-known:

Theorem 1. Let \(\gamma\) be any finite-dimensional irreducible representation of \(G\). Then \(\gamma\) appears as a direct summand of \(V^{\otimes n}\) for some \(n\gg 0\).

The usual proof of this uses analysis; today I want to record a short argument using a bit of algebraic geometry. This came up recently in a little discussion on Twitter with Noah Snyder. In fact, this argument will give the following, over arbitrary infinite fields:

Theorem 2. Let \(\rho: G\to GL(V)\) be a faithful representation, where \(V\) is a finite-dimensional vector space over an infinite field \(k\). Let \(\gamma\) be an irreducible representation of \(G\). Then \(\gamma\) appears as a quotient representation (resp. sub-representation) of \(V^{\otimes n}\) for some \(n\gg 0\).

Note that \(\gamma\) might not be a direct summand.

We’ll need the following representation-theoretic fact:

Lemma. Any irreducible representation of \(G\) is a quotient of the regular representation \(k[G]\). Any irreducible representation is also a sub of \(k[G]\).

Proof of Lemma. There is a natural isomorphism \(\operatorname{Hom}_{k[G]}(k[G], V)=V\) for any representaion \(V\). Thus any non-zero representation admits a non-zero map from the regular representation. If \(V\) is irreducible, such a map is necessarily surjective (as the image is a subrepresentation), giving the first claim. The second claim follows by applying the same argument to the dual representation, and then dualizing (using the autoduality of the regular representation).

Proof of Theorem 2. As the action of \(G\) on \(V\) is faithful, the set \(V^g\) of vectors fixed by a given non-identity \(g\in G\) is a proper Zariski-closed subset of \(V\) for each \(g\in G\). Hence for a general element \(v\in V\), \(G\) acts faithfully on \(v\). Fix such an element of \(V\), and let \(X\) be its orbit under \(G\). As a \(G\)-set, \(X\) is isomorphic to \(G\) with the left translation action.

Now set \(R=\text{Sym}^*(V^\vee)\). Viewing \(X\) as a closed subvariety of $$V=\text{Spec}(R),$$ we get a surjective map $$R\to k[X].$$ But \(k[X]\) is the regular representation! So every irreducible representation of \(G\) appears as a quotient of \(k[X]\) and hence of \(\text{Sym}^n(V^\vee)\) for some \(n\). Dualizing, every irreducible representation appears as a subrepresentation of \(\text{Sym}^n(V^\vee)^\vee\), which is a subrepresentation of \(V^{\otimes n}\), for some \(n\). Applying the same argument with \(V^\vee\) yields every representation as a quotient. \(\square\)

The geometry of the Sylow theorems

Today I want to explain some algebro-geometric manifestations of the Sylow theorems. This blog post is an expansion of a Twitter Thread I wrote a few months ago, which you can find unrolled here.

The Sylow Theorems and some examples

Let’s start by reminding ourselves what the Sylow theorems say, and think about a few examples. Throughout \(G\) will be a finite group and \(p\) will be a prime.

Theorem 1. There exists a subgroup \(H\subset G\) of order a power of \(p\) such that the index \([G:H]\) is prime to \(p\).

Theorem 2. All such subgroups are conjugate to one another.

Theorem 3. The number of such subgroups is congruent to \(1\) modulo \(p\).

Before diving into the meat of this post, let’s just work through this with a couple examples.

Example 1. Let \(G=S_4\) be the symmetric group on four letters. This group has order \(24=2^3\cdot 3\), so we would like to find and analyze subgroups of order 8 and 3 (which are maximal \(p\)-subgroups for \(p=2, 3\)). I like to visualize \(S_4\) via its action on the tetrahedron, pictured below.

The 3-Sylow subgroups are clear visually — they are the stabilizers of the faces, generated by the rotation pictured below. There are four such (one for each face), and they are conjugate because \(S_4\) evidently acts transitively on the faces.

The 2-Sylows are a little harder to see — they’re the stabilizers of the pairs of opposite edges (colored identically below). They are generated by the reflections across the planes containing one edge and the midpoint of the opposite edge, and the “twist” which exchanges two identically colored edges. There are 3 such groups, and they are conjugate because \(S_4\) acts transitively on the set of pairs of disjoint edges.

Example 2. Let \(G=A_5\) be the alternating group on five letters; this is also the group of rotational symmetries of the icosahedron, pictured below.

The order of \(A_5\) is \(60=2^2\cdot 3\cdot 5\), so we’re looking for subgroups of order 3,4, and 5. The subgroups of order 3 and 5 are not so hard to find — they’re given by rotation about an axis through two opposite faces/vertices, respectively, as pictured below.

There are six pairs of opposite vertices, hence six 5-Sylow subgroups; they are all conjugate as \(A_5\) acts transitively on the set of vertices of the icosahedron. There are ten pairs of opposite faces, hence ten 3-Sylow subgroups; they are conjugate as \(A_5\) acts transitively on the set of faces of the icosahedron.

The 2-Sylow subgroup, of order 4, is a little harder to find. Consider a set of four faces sharing no vertices, pictured in green below. Connecting their centers gives a tetrahedron, as pictured.

The subgroup of \(A_5\) preserving the tetrahedron is isomorphic to \(A_4\), and as before, the 2-Sylow (which has order 4) is the subgroup preserving two disjoint edges of the tetrahedron.

By the way, you might wonder where the isomorphism between \(A_5\) and the group of rotational symmetries of the icosahedron arises from — it’s from the tetrahedron above. The tetrahedron was given by choosing four disjoint faces of the icosahedron; there are 5 such choices, giving rise to five inscribed tetrahedra, pictured below somewhat messily. The action of the group of rotational symmetries of the icosahedron on these five tetrahedra gives rise to the isomorphism with \(A_5\).

Example 3. Let’s think about \(GL_3(\mathbb{F}_2)\), the group of automorphisms of the Fano plane, pictured below (this is the set of 1-dimensional subspaces of \(\mathbb{F}_2^3\), labeled by the unique non-zero vector in the given subspace; the lines/circle represent 2-dimensional subspaces containing a given 1-dimensional subspace). This group is also isomorphic to \(PSL_2(\mathbb{F}_7)=SL_2(\mathbb{F}_7)/\{\pm 1\}\).

This group has order 168. To see this, note that we’re trying to count \(3\times 3\) invertible matrices over \(\mathbb{F}_2\). The first column can be any non-zero vector; there are \(2^3-1\) choices for this vector. The second column can be any vector not in the span of the first; there are \(2^3-2\) choices. Finally, the third column can be any vector not in the span of the first two; there are \(2^3-4\) choices. So we have $$\#GL_3(\mathbb{F}_2)=(2^3-1)(2^3-2)(2^3-4)=168.$$

As \(168=7\cdot 3 \cdot 2^3\), we are looking for a 7-Sylow, a 3-Sylow, and a 2-Sylow subgroup. Here a 2-Sylow subgroup is easy to find; it’s given by upper triangular matrices with one’s on the diagonal: $$\begin{pmatrix} 1 & * & * \\ 0 & 1 & * \\ 0 & 0 & 1\end{pmatrix}.$$

To find the 7-Sylow, think of the units of \(\mathbb{F}_8\) acting on \(\mathbb{F}_8\) by multiplication. The units are a cyclic group of order 7, and \(\mathbb{F}_8\) is a 3-dimensional \(\mathbb{F}_2\)-vector space, so choosing a basis of \(\mathbb{F}_8\), we get a 3-dimensional \(\mathbb{F}_2\)-representation of \(\mathbb{F}_8^*\), whose image is precisely the desired 7-Sylow.

3-Sylows work similarly; the units of \(\mathbb{F}_4\) have order 3, and act on \(\mathbb{F}_4\), which is a 2-dimensional \(\mathbb{F}_2\)-vector space. Writing \(\mathbb{F}_4\oplus \mathbb{F}_2\simeq \mathbb{F}_2^3\) and letting \(\mathbb{F}_4^*\) act trivially on the rightmost factor gives a 3-dimensional representation of \(\mathbb{F}_4^*\) whose image is one of the desired 3-Sylows. We could also take a subgroup generated by a cyclic permutation matrix, for example; both constructions generalize well, as we shall see in a future post.

The main example

The main example I’d like to discuss today is a generalization of Example 3 above. Namely, let’s think about $$GL_n(\mathbb{F}_q),$$the group of invertible \(n \times n\) matrices with coefficients in \(\mathbb{F}_q\), for \(q=p^r\) a prime power. As before, we first compute the size of this group. Again, the first column can be any non-zero vector; the second column can be any vector not in the span of the first; the third can be any not in the span of the first two, and so on. This gives

$$\#GL_n(\mathbb{F}_q)=(q^n-1)(q^n-q)(q^n-q^2)\cdots(q^n-q^{n-1}).$$

The easiest Sylow subgroups to find are the \(p\)-Sylows, where \(q\) is a power of \(p\). The largest power of \(p\) dividing the order of our group is $$q\cdot q^2\cdots q^{n-1}=q^{n(n-1)/2},$$ and there’s a pretty easy-to-find subgroup of this size, generalizing what happened for \(n=3, p=2\). Namely, we can again consider the upper-triangular matrices with one’s on the diagonal:

$$\begin{pmatrix} 1 & * & * & \cdots & * \\ 0 & 1 & * & \cdots & \\ 0 & 0 & \ddots & \ddots & \vdots \\ 0 & \cdots & 0 & 1 & *\\ 0 & \cdots & 0 & 0 & 1 \end{pmatrix}.$$

This kind of subgroup has a name — it’s called a maximal unipotent subgroup. Let’s describe such things geometrically.

A flag \(0=F^0\subset F^1 \subset \cdots \subset F^n=V\) inside of a vector space \(V\) is a collection of subspaces, each contained in the next. A full flag is such a collection where each \(F^i\) has dimension \(i\). For \(k\) a field, a maximal unipotent subgroup of \(GL_n(k)\) is precisely the subgroup of the stabilizer of some flag \(F^\bullet\) acting trivially on \(F^i/F^{i-1}\) for each \(i\).

A full flag in \(\mathbb{R}^3\)

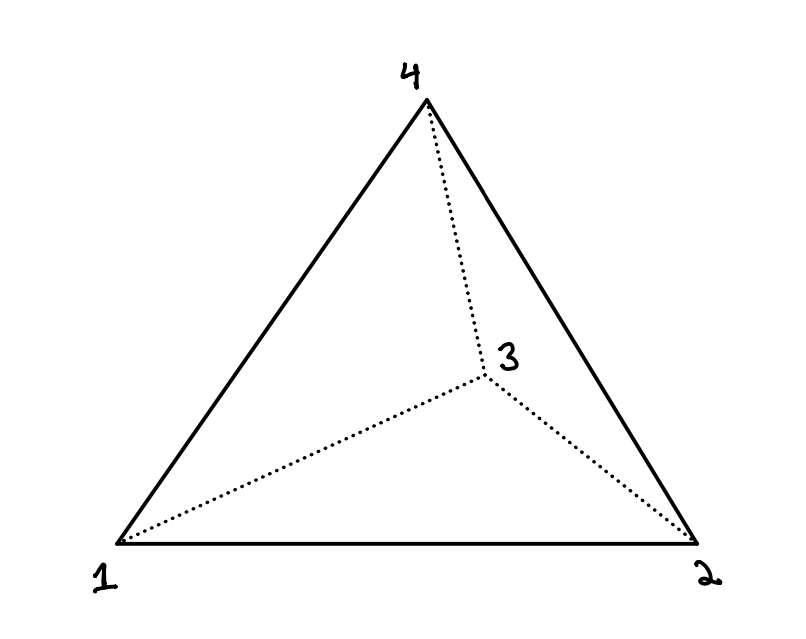
How many full flags (and hence how many maximal unipotent subgroups, aka \(p\)-Sylows, are there) in \(\mathbb{F}_q^n\)? I claim that there are $$(1+q)(1+q+q^2)\cdots (1+q+q^2+\cdots +q^{n-1})=\prod_{i=1}^{n} \frac{1-q^i}{1-q}.$$ Let’s prove this by induction.

The base case where \(n=1\) is trivial — there’s a unique full flag. Now let \(V\) be an \(n\)-dimensional vector space over \(\mathbb{F}_q\). Each codimension \(1\) subspace contains $$\prod_{i=1}^{n-1} \frac{1-q^i}{1-q}$$ full flags by the induction hypothesis, so it’s enough to show that there are $$\frac{1-q^n}{1-q}$$ codimension \(1\) subspaces. Such a subspace is the vanishing locus of a non-zero linear functional, well-defined up to scaling; there are \(q^n-1\) non-zero linear functionals and modding out by scaling by \(\mathbb{F}_q^*\) gives $$\frac{1-q^n}{1-q}$$ as desired.

Let’s check Sylow’s third theorem: $$(1+q)(1+q+q^2)\cdots (1+q+q^2+\cdots +q^{n-1})$$ is equal to 1 mod \(p\), as desired.

A geometric analogue

My student Sasha Shmakov made the following observation to me a few months ago: for \(k\) any field, maximal unipotent subgroups of \(GL_n(k)\) exist and are all conjugate to one another; this is some kind of algebro-geometric analogue of the first two Sylow theorems, at least for \(p\)-Sylows of \(GL_n(\mathbb{F}_q)\). To see this, note that full flags exist inside of \(k^n\), and \(GL_n(k)\) acts transitively on them.

He asked: what’s the analogue of the third Sylow theorem? Amazingly, it turns out there is one.

Instead of counting maximal unipotent subgroups (which we can’t do — if \(k\) is infinite, there are infinitely many of them!) we’ll study the parameter space of maximal unipotent subgroups, or equivalently full flags. This is called the full flag variety \(\text{Fl}_{1, 2, \cdots, n}\).

Let’s write \(G=GL_n\) and let \(B\subset G\) be the stabilizer of a full flag; this is the normalizer of a maximal unipotent subgroup, and is often called a Borel subgroup. The quotient $$\text{Fl}_{1, 2, \cdots, n}:=G/B$$ is (more or less by the orbit stabilizer theorem) the space of full flags; it’s not obvious but it follows from general theory that this quotient naturally has the structure of an algebraic variety.

Let’s work out the geometry of these varieties.

The argument proceeds analogously to the situation over finite fields. Let \(G(n-1, n)\) be the space of codimension 1 subspaces of \(V\). There is a map $$\text{Fl}_{1, 2, \cdots, n}\to G(n-1, n)$$ given by forgetting all but the last subspace of our flag. The fibers of this map over a given codimension 1 subspace \(V’\subset V\) are precisely the full flags on \(V’\), so let’s work out the geometry of \(G(n-1,n)\); this will suffice by induction. But \(G(n-1, n)\) is the space of codimension 1 subspaces of an \(n\)-dimensional vector space, or equivalently the space of lines in \(V^\vee\), so it’s isomorphic to the projective space \(\mathbb{P}^n\).

We can suggestively write $$\mathbb{P}^n=\frac{\mathbb{A}^{n+1}-\text{pt}}{\mathbb{G}_m},$$ where $$\mathbb{G}_m=\mathbb{A}^1- \text{pt}$$ is the multiplicative group of \(k\). This should perhaps remind you of the terms $$\frac{1-q^i}{1-q}$$ appearing in the finite field setting. And indeed, an analogous argument to that case shows that $$\mathbb{P}^n=\mathbb{A}^n\cup \mathbb{A}^{n-1}\cup \cdots\cup \text{pt},$$ that is, the geometric series formula from before makes sense geometrically.

For the experts: we’ve shown that the map $$\text{Fl}_{1, 2, \cdots, n}\to G(n-1, n)$$ has fibers isomorphic to flag varieties, but it’s perhaps not obvious that this bundle is Zariski-locally trivial. There are a number of ways to see this but I think the easiest is to observe that this follows from (Grothendieck’s form of) Hilbert’s Theorem 90.

Formulating the third Sylow theorem

We’re now ready to make sense of a geometric formulation of the third Sylow theorem. We’re going to work in the Grothendieck Ring of Varieties over \(k\), denoted \(K_0(\text{Var}_k)\). This is the free Abelian group on isomorphism classes of varieties \([X]\) over \(k\), modulo the relation that $$[X]=[Y]+[X\setminus Y]$$ for \(Y\subset X\) a closed subvariety. Mutliplication just comes from the Cartesian product: $$[X]\cdot [Y]=[X\times Y].$$ This ring has a distinguished element $$\mathbb{L}:=[\mathbb{A}^1],$$ the class of the affine line.

So for example, from what we observed above, we have $$[\mathbb{P}^n]=\mathbb{L}^n+\mathbb{L}^{n-1}+\cdots+1.$$ And indeed, the argument from above (plus the Zariski-local triviality of the fiber bundle $$\text{Fl}_{1, 2, \cdots, n}\to G(n-1, n)$$ discussed in the last paragraph of the previous section), we can write $$[\text{Fl}_{1, 2, \cdots, n}] = \prod_{i=1}^n (1+\mathbb{L}+\cdots +\mathbb{L}^{i-1})$$ in \(K_0(\text{Var}_k)\), exactly in analogy to the situation over finite fields.

So here is an analogue of the third Sylow theorem, which we’ve just proven:

Theorem. We have $$[\text{Fl}_{1, 2, \cdots, n}]= 1 \bmod (\mathbb{L})$$ in \(K_0(\text{Var}_k)\).

That is, the space of maximal unipotent subgroups in \(GL_n\) — which we can perhaps think of as \(\mathbb{L}\)-Sylow subgroups — is congruent to 1 modulo \(\mathbb{L}\). In fact — for the experts — the analogous statement holds for split reductive groups over any field.

In a future post I’ll discuss analogies for prime-to-\(p\) Sylows, and what happens for non-split groups, where things get substantially more complicated!

Some low-hanging fruit

Today is the #ShutdownSTEM strike, a day when non-black members of the academy strike in solidarity with the black lives matter movement, and take action to work to improve STEM academia. To quote their website:

“Those of us who are not Black, particularly those of us who are white, play a key role in perpetuating systemic racism. Direct actions are needed to stop this injustice. Unless you engage directly with eliminating racism, you are perpetuating it. This moment calls for profound and meaningful change. #ShutDownAcademia and #ShutDownSTEM is the time for white and non-Black People of Color (NBPOC) to not only educate themselves, but to define a detailed plan of action to carry forward. Wednesday June 10, 2020 will mark the day that we transition into a lifelong commitment of actions to eradicate anti-Black racism in academia and STEM. ”

— #ShutdownSTEM

I wanted to briefly share a few easy things you can do if, like me, you’re a pure mathematician participating in the strike today. I’ve tried to limit myself to listing only concrete deliverables that you can achieve today, while sitting at your computer; this is somewhat counter to the spirit of the strike, which suggests we “define a detailed plan of action to carry forward”— that’s something I’m still thinking hard about. I’ve also avoided suggesting e.g. readings or academic literature on race and math education, not because I think this is a bad idea, but because I don’t feel qualified to make recommendations in this area. And of course anything you can do today, while sitting at your computer, can only have a tiny impact on the margin; this document is only meant to identify the lowest of the low-hanging fruit — mostly emails and donations.

With that said, here are some things you can do:

• Join or donate to the National Association of Mathematicians, which aims to “[promote] excellence in the mathematical sciences” and “[promote] the mathematical development of all underrepresented minorities.” Email your department chair and suggest that your department get an institutional membership (150 dollars). If you have money to spare, offer to sponsor memberships for some number of graduate students in your department (30 dollars per student), and ask your colleagues to do the same.

• Donate to Mathematically Gifted and Black, which supports “predoctoral mathematicians to pursue career goals related to the mathematical sciences.”

• Learn a bit about the history of racism in mathematics, and encourage the AMS and your department to make restitution. Here’s a good place to start (if you’re at UGA like me, note that we feature prominently and embarrassingly) — h/t Jesse Kass.

• Along similar lines, try to figure out if any buildings on your campus are named after famous bigots. At this point I think it’s fairly well-known that the math department at UT Austin is named after R.L. Moore, who was extremely bad. Several minutes of googling led me to Joseph E. Brown Hall, the Richard B. Russell Building, LeConte Hall, Baldwin Hall, and Candler Hall at my institution, UGA. If the president of your university has just released a statement reaffirming the university’s “commitment to diversity and inclusion,” it might be worth replying with a suggestion to change the names of such buildings. In my view this is more than just a symbolic act — I can only imagine how unpleasant it would be to live or work in a building named after someone dedicated to enslaving your ancestors. Unfortunately, it seems quite hard to get a building name changed (at UGA it seems to require a vote of the Board of Regents, and at some other state institutions it apparently requires a vote of the state legislature(!)), but sending an email can’t hurt.

• It’s not clear to me whether this is in the spirit of #ShutdownSTEM (part of which is not doing any research for the day), but take a look at some papers written by black mathematicians in your field. In algebraic geometry and number theory, you might start by looking at Kevin Corlette’s work on non-abelian Hodge theory and Adebisi Agboola’s work on Iwasawa theory, respectively (obviously this is far from an exhaustive list). Here’s a useful resource.

• Do you know any black graduate students who might be a good fit as postdocs at your department? Or black postdocs who might be a good fit as tenure-track faculty at your department? If so, it might be good to start laying some groundwork for that to happen — for example, invite them to give a talk in your seminar and mention them to your colleagues, and be prepared to suggest they apply when the time comes. If not, that’s bad — you might think about how to change that.

Again, this is a pretty tiny proportion of what one should do, but the point I wanted to make by writing it is that some small actions are actually pretty easy. Even though the payoff is likewise small, I thought these ideas were worth sharing. Please let me know if you have any comments, corrections, or suggestions.

Scissors integration

On Twitter Sarah Griffith made the following wonderful observation:

Maybe this doesn't seem strange to anyone else, but I just realized I find it very strange that if you integrate a polynomial over Q between rational bounds you always get a rational number, even though the area under the curve can be quite complicated

— Canonically Singular Sarah (@SC_Griffith) April 29, 2020

Indeed, I think this fact — that the integral of a rational polynomial in one variable between rational bounds is rational — is very non-obvious geometrically, even though it’s clear from the fundamental theorem of calculus!

Why does this region have rational area?

I came up with a synthetic proof, which I want to share here. It give a geometric proof of the fundamental theorem of calculus for polynomials, which I think is pretty cool, but it also proves more, and points in the direction of some interesting generalizations.

Here’s the argument. By linearity of the integral, it’s enough to show that $$\int_0^a x^n dx=\frac{a^{n+1}}{n+1}$$ for all rational \(a\) and all non-negative integers \(n\). Now \(x^n\) is the volume of an \(n\)-cube with side length \(x\); hence $$\int_0^a x^n dx$$ is the volume of a figure swept out by a growing \(n\)-cube, with side length ranging from \(0\) to \(a\).

So for example the figure below, swept out by an expanding square, computes the integral $$\int_0^a x^2 dx.$$

Integating \(x^2\)

I claim that this figure can be dissected into \(n!\) \(n+1\)-simplices, each of which has volume $$\frac{a^{n+1}}{(n+1)!}.$$ Hence its total volume is $$n!\cdot \frac{a^{n+1}}{(n+1)!}=\frac{a^{n+1}}{n+1}$$ as claimed.

We first show that the volume of an \(n+1\)-simplex with side length \(a\) is \(\frac{a^{n+1}}{(n+1)!}\), as claimed. It suffices to show that an \(n+1\)-cube of side length \(a\) (which has volume \(a^n\)) can be dissected into \((n+1)!\) congruent \(n+1\)-simplices. But we can view the cube as the region $$0\leq x_1, \cdots, x_{n+1} \leq a.$$ Then for any element \(\sigma\) of the symmetric group on \(n+1\) letters, the region $$0\leq x_{\sigma(1)}\leq \cdots \leq x_{\sigma(n+1)}\leq a$$ is a simplex with side length \(a\), and these \((n+1)!\) simplices evidently fill up the \(n+1\)-cube and intersect only along their faces. The action of the symmetric group shows the simplices are all congruent.

Now why does our figure (swept out by a growing \(n\)-cube) admit a dissection into \(n!\) \(n+1\)-simplices? It’s because the \(n\)-cube can be dissected into \(n!\) simplices by what we just did, and each of these sweeps out an \(n+1\)-simplex! So we’re done.

A dissection of our region into \(2!\) \(3\)-simplices

By the way, @yougetaquote also found a beautiful (and closely related) probabilistic argument:

so this probability is our integral. But it is also clearly equal to 1/(n+1) since the prob of each guy being the maximum is the same.

— Stevie Tieta - formerly Oprah Quotes (@yougetaquote) May 2, 2020

Scissors integrals

I claim this argument actually proves something more, which I think is pretty cool — the point is that because it works entirely via dissection, it actually proves something in the “scissors congruence” group. As a reminder, the scissors congruence group for \(\mathbb{R}^n\), denoted \(S(n)\) is the free Abelian group on the set of \(n\)-dimensional polytopes in \(\mathbb{R}^n\), modulo the following relations:

1. \([P]=[P_1]+[P_2]\) if \(P\) can be dissected into \(P_1, P_2\), and

2. \([P]=[gP]\) for \(g\) any isometry of \(\mathbb{R}^n\) (for the usual metric).

The direct sum $$R=\bigoplus_n S(n)$$ forms a graded ring (under Cartesian product of polytopes). Throughout the rest of this section I’ll freely identify a \(d\)-dimensional polytope contained in a \(d\)-plane inside of \(\mathbb{R}^n\) with the corresponding polytope in \(\mathbb{R}^d\).

I would like to think of a polytope \(P\) as analogous to a monomial, and describe a way of integrating it over various regions, to get new elements of \(R\). Namely, let \(G_n\) be the subgroup of automorphisms (not isometries!) of \(\mathbb{R}^n\) generated by scalings and translations. That is, $G_n$ is the subgroup of affine-linear transformations of the form $$(x_1, \cdots, x_n)\mapsto (a_1x_1+b_1, \cdots, a_nx_n+b_n)$$ with the $a_i$ positive. There is an evident isomorphism $$G_n\simeq \mathbb{R}^n\rtimes \mathbb{R}^n,$$ where the transformation above maps to $$(b_1, \cdots, b_n, \log a_1, \cdots, \log a_n).$$ I’ll choose the evident identification of this with \(\mathbb{R}^{2n}\).

Now let \(D\subset G_n\) be any \(d\)-dimensional polytope, under the identification of \(G_n\) with \(\mathbb{R}^{2n}\) above. Then for an \(n\)-dimensional polytope \(P\) in \(\mathbb{R}^n\), I will define the scissors integral $$\int_{D}^{SC} P:=\left[\bigcup_{d\in D} (d, dP)\subset \mathbb{R}^{2n}\times \mathbb{R}^n\right]$$ to be the class of the \(n+d\)-dimensional polytope defined above. We may of course also let \(P\) or \(D\) be linear combinations of polytopes, and extend the definition bilinearly.

Note: It’s not clear to me how this depends on \(D\) and \(P\); for example, there are some natural (scissor-type) relations on \(D, P\) so that the integral only depends on the congruence-class of \(D, P\). It would be very interesting to work out the maximal (or a large) set of relations for which this is true.

How does this relate to the stuff above? There’s a very natural 1-dimensional polytope in \(G_n\) for each \(n\), which I’ll denote \([a, b]\) (suppressing the dependence on \(n\)). This consists of maps of the form $$(x_1, \cdots, x_n)\mapsto (cx_1, \cdots, cx_n)$$ for \(a\leq c\leq b\). With some good will, I hope you’ll let me denote $$\int_a^b P dP:= \int^{SC}_{[a,b]} P.$$

There’s also an extremely natural polytope $$\mathbb{x}\subset \mathbb{R}, \mathbb{x}:=[0,1],$$ and for any non-negative real number \(a\) I’ll let $$[a]:=a\mathbb{x}=[0, a].$$

Then the argument above in fact shows $$(n+1)\int_a^b \mathbb{x}^n d\mathbb{x}=[b]^{n+1}-[a]^{n+1}.$$

This is a scissors fundamental theorem of calculus! One obtains the usual fundamental theorem of calculus (for polynomials) by applying the function that sends a (scissors congruence class of) polytope to its volume.

You’ll note that I multiplied by \(n+1\) on the left side of the equation, rather than dividing on the right as one might usually do. That’s because this is what the argument actually gives, and I’m not sure if \(SC(n+1)\) (where both sides of the equation live) is uniquely divisible. For \(n=0,1,2\), they are, and so one can divide both sides by \(n+1\). [EDIT: Sasha Shmakov points out to me that \(SC(n)\) is actually a real vector space, and hence clearly uniquely divisible, so you can divide by \(n+1\) if you want.]

What other integrals can you compute? How does the integral change as one varies \(P, D\)? I’ll let you know when I think about this more myself! In particular, I find it very plausible that there’s a “fundamental theorem of calculus” for a much broader class of polytopes \(P, D\).

Grant Materials

I was recently funded by the NSF Algebra and Number Theory grant DMS-2001196. Since other people may find it useful, I figured I would post my proposal here. I don’t claim at all that this is a model proposal, and there are a lot of changes I would make in retrospect, but hopefully it is useful to other people applying for grants.

Department tea, and revised office hours tomorrow.

Two quick announcements. One is that I’ll be hosting department teas for the UGA math department on Zoom, starting next Wednesday. You can find the schedule and Zoom link here; if you think you should have the password (i.e. if you’re a member of the UGA math department), and you don’t have it, please email me.

Second announcement — I’ve now posted a schedule for office hours here, as well as the Zoom link. Please feel free to join if you are at all interested in arithmetic or algebraic geometry; this isn’t just for UGA students. Please note that the time for office hours tomorrow is slightly unusual; rather than taking place from 2-4pm EDT, it will take place from 1-3pm EDT, due to the UGA math department award ceremony taking place at 3pm tomorrow. After tomorrow, the schedule will return to usual.

WAGON: Lessons learned

This past weekend was the first-ever WAGON conference (Western Algebraic Geometry ONline), which was meant as the online iteration of the Western Algebraic Geometry Symposium (WAGS). Here “Western” refers to the western United States (which is typically the area from which WAGS draws attendees), but the conference ended up attracting participants from all over the world — I think it was plausibly the largest algebraic geometry conference since the Utah mega-conference in 2015, with over 1000 registrants and up to 700 participants there at any given time. 

The conference was organized by Jarod Alper, Isabel Vogt, and myself; I joined, despite not living in the western US, because of my experience organizing AGONIZE (which was one of the first online AG conferences to take place after the COVID pandemic began). I wanted to use this thread to discuss what worked and what didn’t, what I learned from both AGONIZE and WAGON, and to summarize and discuss some comments from participants. I’ve tried to focus to some extent on areas for improvement, even though I found the conference to be an extremely positive experience, since that’s what I think this kind of document is useful for. And I am writing from the point of view of an early-career faculty member, so while I’ve tried to be sensitive to the concerns of e.g. postdocs and graduate students, as well as those of more senior people, I’ll inevitably miss some things — please know that I welcome comments or suggestions, either in the comments below this post or via email. You can reach me at dlitt[AT]uga.edu.

Table of contents

• Technology and participation

• The format of the conference

  • The talks

  • The social events

  • The panels

• Scheduling

  • Weekend conferences

  • Time zones and talk scheduling

• Conclusions

The conference poster

Technology and participation

The conference was hosted with a Zoom Webinar 1000 license, generously provided at no cost by Stanford. This license can accommodate up to 1000 non-video participants at any given time, as well as up to 100 participants with video; Zoom automatically handles registration, and sends a link to each registrant. Over a thousand people (1105, to be precise) registered for the conference, and I would guess that about this many people dropped by. At any given time, there were 200-700 participants. The median session had 400 unique viewers, though the plenaries were consistently well over this. Despite the large number of participants, there were no issues with Zoom-bombing or bad behavior. Participants came from all over the world — one attendee, joining from Japan, mentioned that he had begun adjusting his sleep schedule several days prior so that he could be awake for talks taking place at 330am local time.

I just witnessed the most successful math conference I've ever seen, and it was entirely online, even the coffee breaks.

Could it be that this might be a better system for doing mathematics?

— Cathy O'Neil (@mathbabedotorg) April 20, 2020

Unlike an in-person conference, WAGON cost nothing to organize (or attend); depending on one’s institution and the size of the conference one is planning, the Zoom Webinar license might cost on the order of 1000-2000 dollars. It was organized over the 3-4 weeks prior to the event.

The conference was advertised widely, on the usual mailing lists and conference websites, as well as more recent innovations like mathseminars.org, but not, I think, more widely than the usual pre-COVID conference. In part the massive participation speaks to the low barriers to attend the conference — no travel required — but it speaks also, I believe, to a real need in the community.

The format of the conference

The event consisted of two hour-long plenary talks (delivered by János Kollár and Claire Voisin), six 25-minute talks (delivered by Nick Addington, Juliette Bruce, Johan de Jong, Ariyan Javanpeykar, Valentijn Karemaker, and Mauricio Velasco), two panels, and various social events. 

The conference schedule

The talks

The talks were of the highest quality. All of the speakers except for Voisin opted to use slides, with some of them annotating the slides (using a stylus) as they spoke. Voisin used a whiteboard with a webcam pointed at it, which worked fairly well, though there was initially some difficulty reading what was written (especially small subscripts or when the marker started running out of ink).

I think it's close to 31 years since I first heard a talk by Claire Voisin. I was impressed then, and I've been impressed every time I heard her since. #wagon2020

— Scoffing Mathematician 🏳️‍🌈🇪🇺 (@BarbaraFantechi) April 19, 2020

One of the major downsides of a virtual conference is that talks lack the interactivity of a usual conference — especially in algebraic geometry, talks tend to be rambunctious, with lots of interruptions from the audience. Technological necessity (as well as the large numbers of attendees) meant that this wasn’t really possible. That said Zoom allows several mechanisms by which attendees can ask questions:

1. Chat: we encouraged participants to use this primarily to ask questions of other participants, and there was a lively discussion throughout most talks. In addition the organizers generally kept an eye on the chat and scanned for interesting questions for the speakers.

2. Q&A: the Zoom Webinar format allows participants to write questions which are only visible to the speaker or panelists. From past experience (i.e. AGONIZE) we found that asking the speaker to keep an eye on Q&A/chat was very distracting, so one of the organizers was tasked with moderating the Q&A, textually answering some questions, and interrupting the speaker with especially urgent questions; other questions were held to the end. For short talks, all questions were held to the end.

3. Hand-raising: Zoom allows attendees to “raise their hand,” after which an organizer can unmute them and they can ask a question verbally. This feature was used in some of the talks, though several participants “raised their hand” by mistake.

At AGONIZE we had an additional discussion platform — namely a Google Doc that participants could use to discuss the talk as it went on; this was Ravi Vakil’s innovation. We opted not to use a similar strategy at WAGON because of Google Doc’s serious technological limitations: no more than 100 or so people can edit a document at once, so this technique is unusable for large conferences.

Zoom’s chat is very bare-bones. In particular, participants were unable to chat privately with one another, or even to know who else was in the room with them! In retrospect it might have been better to use an external chat client like Slack or Discord. That said there was usually a lively (public) discussion of mathematical questions which arose during the talks.

There was no side chatter. I usually sit next to someone like @xanderfaber at talks, and then I whisper my dumb questions to him (esp at algebraic geom talks). Or we make silly comments. Or he mutters "that's baller" under his breath. There was no way to do this.

— Dr. Wandering Point (@WanderingPoint) April 21, 2020

I found moderating the chat and Q&A to be quite exhausting. There is a fair amount of improvisation required, and some risk — during Voisin’s talk, my co-organizer Isabel’s internet cut out while she was moderating, though luckily this didn’t last for too long (and my co-organizer Jarod stepped in to fill the gap). One participant suggested that the extent to which the Q&A would be moderated should have been made more clear before the conference — I or others in chat ended up answering some questions which were intended for speakers, which might have been jarring. I think substantial moderation is inevitable in such a large event, but I would love to hear alternate suggestions. I imagine that too-heavy-handed moderation, or its opposite, would have the possibility of harming a talk, though I don’t think this happened to us.

Despite these (in my view minor) difficulties, I found the talks really enjoyable and enlightening, and I think this sentiment was common among the participants.

#wagon2020
I think this is the best thing happens during lockdown in my country. Thanks for all the efforts for bringing this conference.

— By✵Your✵Side (@ting__ss) April 18, 2020

A screenshot from Nick Addington’s talk.

The social events

One of the major experiments attempted at WAGON aimed to simulate some of the more informal aspects of an in-person conference — meeting random people at coffee, getting lunch with your friends, bumping into a collaborator, etc. We asked a range of people (senior colleagues, graduate students, postdocs, my NSF program officer) to host their own Zoom “tables” during the coffee break, lunch break, and reception. Links to these rooms were posted in a Google Doc; as rooms got more crowded, other participants could (and did!) create new tables on the fly.

The coffee break Google Doc

As participants entered and exited each table, we asked them to put their names on the Google Doc, so people could find their friends, or people to whom they wanted to ask questions, etc. This happened less reliably, though some of the table hosts did regularly update the Doc with the names of those who had joined their table.

Overall I think this experiment was a success — all of the tables I joined had lively discussion, often with 10-15 active participants, and there were 6-8 tables during each break. Discussions topics ranged from mathematics, to COVID, to small talk, to the conference itself. Michelle Manes hosted a Q&A about NSF funding; Will Sawin wandered from table to table searching for problems to solve. It was great.

As far as I know the only technical hiccup was the Google Doc, which hung as hundreds of people tried to edit it. This is a problem which surely has a technical solution. If anyone can suggest (or engineer) one, I would be very grateful.

In the future I would change a few aspects of this system. First, it’s not clear to me that asking participants to record which table they are at is actually useful — for one, I think it is a request which is doomed to be ignored. But for another, I think it to some extent encourages cliquishness, and makes it more difficult to join a table at which you don’t recognize any names. Indeed, some junior participants suggested that they found it intimidating to try to join any of the rooms during the social events.

Trying to join a table at #wagon2020 is very intimidating :o

— Michael Klyachman (@MKlyachman) April 18, 2020

But, the tables... I did the following: I mostly joined tables organized by people I knew. And when I was there I mostly talked to people I knew. And where did I know these people from? Other in-person conferences where we met & got to know each other.

— Dr. Wandering Point (@WanderingPoint) April 21, 2020

That said, other junior participants wrote to say that the social events were their favorite part of the conference. Several junior people hosted well-attended Zoom rooms during multiple breaks, and a couple of participants mentioned that they were thrilled to be able to join a Zoom room with the speakers after their talks, so that they could ask any questions which came up.

Dr. Wandering Point (quoted above) also suggested that the coffee breaks were a bit too short, and I agree. At an in-person coffee break one can chat with other attendees while in line; here one had to step away from the computer to make coffee, at which point the break would be almost over.

In general I think we could have done a better job of indicating that it was OK to join a room to just chat, or without a burning math question — again, some junior participants mentioned that they felt they had to have a specific mathematical issue to discuss with their senior colleagues before entering a conversation. I worry that I enjoyed the social events because I knew so many of the participants; if you’re a junior attendee reading this, I’d love to hear what you think we can do to improve the social experience in the future. Of course this issue might not be unique to virtual conferences.

And one aspect of an in-person conference it is impossible to emulate online is the concessions — I think my co-organizer Jarod and I were the only participants drinking a beer during the reception.

My personal experience of the social events was fantastic, and I think they were a clear improvement over not having social events. It was wonderful to see colleagues and friends from all over the world, many of whom I had planned to see in upcoming events that have now been canceled. And I think there is a real need for these kinds of events, even if they are imperfect — I miss the greater math community a great deal, and even if it requires some awkward Zoom silences, I’ll take any time I can get.

The panels

We had two panels, one on “Work-life balance while social distancing,” moderated by Dagan Karp and featuring Laure Flapan, Daniel Hernández, Brian Lehmann, and Sam Payne, and the other on “COVID and the profession,” moderated by Ravi Vakil, and featuring Brendan Hassett, Caroline J. Klivans, and Bianca Viray. The former panel focused primarily on more personal aspects of being a mathematician during a pandemic, whereas the latter focused on where the profession is heading, and what we can do to mitigate COVID’s impacts, especially on younger mathematicians.

Q&A and audience participation worked similarly to the talks; chat was extremely active during the panels and the moderators did an excellent job keeping an eye on it. I found both panels very valuable, and I think many participants took comfort from the fact that the panelists discussed the struggles they’ve been facing during these difficult times.

The #wagon2020 panel on work-life balance was so nice! It's relieving to realize that productivity is a struggle for others too, plus there were some really excellent ideas for how to cope.

— D. Zack Garza (@dzackgarza) April 18, 2020

Sam Payne at #wagon2020: You're not doing anything wrong if you're writing and submitting papers, and you're not doing anything wrong if you're *not* writing and submitting papers.

— Daniel Litt (@littmath) April 18, 2020

While I think the panels were both quite useful, especially to those (like me) in reasonably secure positions looking for ways to help those junior to them, there were some real concerns from participants about how these (admittedly very difficult!) topics were addressed. Some junior participants suggested to me that they felt their concerns were ignored to avoid making the panels too depressing, or that questions from the chat were cherry-picked to avoid giving hard answers. And in retrospect it was, in my view, an error to include only tenured faculty on the latter panel. While the panelists had really fantastic insight into the political and financial realities involved in, say, hiring postdocs in the next few months, I think the latter panel might have benefited from a less secure voice. Laure Flapan did an incredible job representing early-career voices on the first panel.

One participant suggested that future iterations of panels along these lines might be “flipped,” with several junior participants and at most one or two senior participants. I would love to see how such a panel plays out.

Scheduling

Weekend conferences

Following the usual WAGS tradition, WAGON took place on a weekend. Nick Addington and others pointed out the irony in having a panel on “work-life balance” during a weekend conference. Especially for those wrangling young kids, it’s difficult to block off an entire weekend to attend a conference at home. Nick suggested that the value of a weekend in-person conference — namely that it’s harder to get away from work during the week — has largely disappeared now that we work from home. Others suggested that they had ways to occupy their kids during the week (e.g. elementary school classes on Zoom), and were parenting on the weekend full time. Possible solutions suggested include: spreading out the conference a bit more — maybe one or two events per day for several (not necessarily consecutive) days, or 4 half-days instead of 2 days.

Of the suggestions discussed (via email, twitter, etc.), I don’t think there was a clear favorite, and in any case the discussion happened too late to significantly change WAGON’s programming. My instinct is that the only solution is to have many different types of events with many different types of schedules, to accommodate as many different lifestyles as possible. No conference can be all things to all people.

Time zones and talk scheduling

Because the conference took place under the WAGS banner, it ran in Pacific Daylight Time, starting at 9am PDT and concluding in the late afternoon PDT. This meant that things were quite convenient for those in the Americas, but that the rest of the world was somewhat inconvenienced. I mentioned earlier that a participant in Japan stayed up into the early morning to attend; anecdotally it seems that a substantial number of attendees came from Europe and Asia, despite the inconvenience.

There was some question as to why we only had two hour-long talks and six short talks, as opposed to the usual WAGS lineup of eight or so hour-long talks. In my view we made the right decision here — all of us have too much screen-time currently, and personally I find attending an online talk much more exhausting than an in-person talk.

Conclusions

It’s impossible to replicate online all that’s good about an in-person conference, and I don’t think that should be our goal. I think we did well at replicating the mathematical aspects of such a conference, and less well at the non-mathematical aspects.

The clear benefit a conference like this has over a traditional conference is the ease with which it can be organized, and attended. Personally, I would like to see more online conferences, even after things return to normal — I think has already begun to some extent (e.g. with the VaNTAGe series).

The main downside WAGON’s talks over traditional (in-person) talks is the lack of interactivity. I think this is a problem which has a solution which is in part technological and in part cultural, and that as we all practice giving and attending online talks we will inevitably see an improvement. I found that the moderated Q&A we used for Kollár’s and Voisin’s talks worked reasonably well.

The non-mathematical aspects of the conference were in my view less of a success, though I still think they were a dramatic improvement over the alternative of omitting them. Many of the problems we faced were magnifications of similar problems faced by in-person conferences. The awkwardness of video chat only makes an atmosphere of inclusivity — already difficult to foster in close proximity — significantly harder to achieve.

Great points in this thread by @WanderingPoint. But I also want to add that coffee & lunch breaks at in-person conferences can have similar problems. The math community doesn't always grapple with this, but we have an opportunity to dream up something better by facing it head on. https://t.co/6T5oeokQmR

— Bianca Viray (@blviray) April 21, 2020

One thing I wish we had done is solicit input from more junior people while planning. For people already embedded in the community, it was easy to find friends during the social events, speak up in chat, etc. But I wonder if the facelessness of an online event makes speaking up more forbidding.

We’ll keep experimenting. I think there’s lots of room for improvement, both technologically and organizationally — the next thing I’d like to try is a workshop-type event, modeled after the Arizona Winter School or the Stacks Project Workshop. Please let me know if you’d be interested in helping to organize this, or in running a working group.

I’ve spent a substantial amount of space here talking about criticisms of the conference, but we also received a huge amount of support, much of which I found very moving. I think there’s a real need in the community right now for events like this, and I had a wonderful time. Again, please let me know if you have any comments, suggestions, or complaints, either in the comments below or via email. I’d love to hear them.

WAGON

For those of you who haven’t yet, you should register for WAGON! Poster below — it’s going to be great.

Reflections on AGONIZE and online conferences

Videos are now up for AGONIZE. I’ve committed to organizing another one of these — stay tuned for more info.

Since this was one of the first math conferences of our new era, I wanted to write a brief reflection on what worked and what (in my opinion) didn’t work.

Technical Aspects

The conference was run as a Zoom meeting — UGA’s Zoom license can accommodate meetings of up to 300 people, which turned out to suffice (and one can purchase more expensive licenses which can handle larger groups). I and each of the speakers were “co-hosts” of the meeting, meaning that we could share our screen and had the power to mute other participants. There were essentially no technical glitches, with two minor exceptions: (1) one of the speakers’ iPad’s briefly stopped screen-sharing, just for a few seconds, and (2) there were some minor audio glitches during one of the talks, but nothing that prevented the speaker from being understandable. Overall, this aspect of the conference went much more smoothly than I expected.

The speakers used a variety of technologies to give their talks. Wanlin shared Beamer slides; Padma shared slides and the switched to writing in the iPad’s Notes app; Hannah pointed a webcam at a blackboard and lectured from the board and then briefly shared a pdf containing some more involved pictures; and Isabel screen-shared from the iPad’s notability app. All of these techniques worked reasonably well — I thought lecturing from the board went surprisingly well, except that colored chalk didn’t show up so well. Isabel’s solution of pre-writing part of her talk in Notability and then filling in parts of it to give a more interactive feel was really excellent, and I plan to imitate it in the future.

I think recording the talks worked well also, as you can see from the videos.

Attendance and Interactivity

Over 250 people registered for the conference — there were between 110 and 130 attendees there at any given time, with people dropping out and others arriving halfway through. The conference took place only a week after it was first advertised (on Twitter, Facebook, Ravi Vakil’s and Kiran Kedlaya’s conference lists, and the Women in Numbers mailing list) so I think this was fairly reasonable.

Overall the audience was well-behaved — large Zoom meetings like this run the risk of being overwhelmed by background noise from participants who haven’t muted themselves. But most participants stayed muted except when asking questions; there were only a few people whom I had to mute remotely. I was also worried about e.g. trolls joining and disrupting the event (which has apparently happened to some online seminars) but we avoided this. I think requiring participants to register before they received a link to the meeting likely helped.

One thing I found a bit disappointing was the audience’s reluctance to ask questions — we originally had planned to let people click the “raise hand” button and wait to be called on if they wanted to ask a question, but people seemed reluctant to do this. Eventually we ended up with a combination of that, as well as a separate Google Doc for questions and discussion, questions asked in chat, and some people who would just unmute themselves and interrupt the speaker. There was not too much of this last method of question-asking, though, so things didn’t devolve into total chaos.

The Google Doc (which I think was suggested by Ravi Vakil during the first talk) was quite interesting. About 70-80 participants had it open at any given time. It was extensively used during the first talk and then usage seemed to slowly drop off. I think people did find it useful — personally I found it distracted me from the talks, though maybe that’s because I was scanning it for questions to ask the speaker in my role as moderator.

To me this is one of two main unsolved problems regarding online conferences — how should participants ask questions? I’d love to hear any thoughts you have.

Social Aspects

The other unsolved problem, in my view, is how to simulate some of the social aspects of conferences (e.g. chatting with other participants during coffee breaks). We tried a few different things. We briefly tried the “breakout room” function of Zoom, whereby people are sorted into random rooms and have some time to chat. I did hear a few positive things about this, but also that some people were put in rooms with 5 or 6 non-responsive people. One possible solution would simply be to make the rooms larger — with 20-person rooms, probably at least a few people will respond.

People did use the chat functionality in Zoom throughout the conference — it’s a bit more primitive than e.g. Slack or Discord, but it’s OK. But chatting was overall somewhat minimal. The Google Doc also filled some social role.

Finally, after the last talk, about 50-60 participants stuck around to discuss how to organize conferences like this, and to give some feedback. Of the 50-60 people who stuck around, probably around 20 contributed to the discussion, which I found pretty valuable. It’s possible that just encouraging participants to turn on their video and unmute themselves during breaks like this would work reasonably well.

Scheduling

One thing I intend to do differently in the future is scheduling. The conference took place from 12pm-5pm EST because some of our speakers live on the West Coast, but this ended up resulting in 4 consecutive talks with only 15-minute breaks between them. That was too much — I, at least, found it pretty exhausting. In the future, I would try to spread out 4-5 talks over a whole day, and not worry too much about participants making it to every talk. In between talks, we could try various ways of imitating the social aspects of an in-person conference, as discussed above.

Comments?

Please let me know if you have any comments or suggestions regarding AGONIZE or its future iterations. Also, please let me know if you have any questions on how to organize something like this for yourself!

Office Hours

Since I’ve been working from home for the last couple of weeks, and will continue to do so for the next few months, I’ve felt a bit starved for mathematical contact — I’m sure many of you feel the same way. So I’m starting weekly office hours, from 2-4pm EST on Fridays. Join me at https://zoom.us/j/831448945.

These office hours are primarily for grad students and postdocs in arithmetic geometry (very broadly construed) — last week we also had a few more senior people drop by. I’d like to keep the discussion at least 50% mathematical, but I’m also open to career questions and any issues of interest to the profession. Hope to see you tomorrow (and weekly thereafter)!

AGONIZE

This post announces the first ever AGONIZE conference (Arithmetic Geometry is ONline In Zoom, Everyone)! The conference will take place Wednesday, March 25, from 12pm-5pm EST. For more info and to register, see the conference website and the conference poster below. We have a really great lineup — I couldn’t be more excited.

Geometricity and Galois actions on fundamental groups

A couple months ago I went to a fantastic conference on Arithmetic Topology at PIMS. The video from my talk is now up: enjoy!

I spend the first few minutes of the talk joking around about this cartoon:

Pictured: Wei Ho, Ravi Vakil, Benson Farb, Jordan Ellenberg, Kirsten Wickelgren, Soren Galatius, Will Sawin, and the Dragon Langlands

I'm a Numberphile!

The popular YouTube channel Numberphile has just released a video featuring yours truly — filming this with Brady Haran was a real pleasure!

A couple of quick mathematical comments: in the video, I compute the Dehn invariant of the cube with side length \(1\) as \(12\otimes \pi/2\) — astute YouTube commenters have already noticed that this is the same as zero! I never really discussed the group structure on \(\mathbb{R}\otimes \mathbb{R}/2\pi\), so I resisted saying this in the video.

For a similar reason, the proof that the Dehn invariant is actually an invariant (under cutting and pasting) sketched in the video is not quite complete. The gap is that I never explain what happens with new edges added (in the middle of what used to be a face) when one makes a cut! The point is that new edges come in pairs with equal length and with dihedral angles which sum to \(\pi\). So the contribution to the Dehn invariant is \[\ell\otimes \theta_1+\ell\otimes \theta_2 =\ell\otimes \pi=0,\] where here I use that \(\ell\otimes \theta=0\) if \(\theta\) is a rational multiple of \(2\pi\).

Anyway, hope you all enjoyed the video!

Arithmetic and Representations of Fundamental Groups

I gave a talk at the IPAM conference “Braids, Resolvent Degree, and Hilbert’s 13th Problem” this past Thursday. The conference was really inspiring — I enjoyed all the talks, but I’d in particular like to recommend Jesse Wolfson’s three talks for a really excellent overview of Hilbert’s 13th problem, Mark Kisin’s talk on recent progress he, Jesse, and Benson Farb have made on the problem, Laure Flapan’s talk for a fascinating overview of her work on Kodaira fibered surfaces (along with some intriguing open questions about them), and Alexander Duncan’s talk on the numerology of essential dimensions of small finite simple groups. Basically, I’m pretty into resolvent degree right now.

My talk, on “Arithmetic and Representations of Fundamental Groups” is below — it starts about 5 minutes in to the video.

Daniel Litt - Institute for Advanced Study, Mathematics We discuss geometric (and function field) analogues of several well-known theorems and conjectures in number theory, including Mazur's torsion theorem, the Fontaine-Mazur finiteness conjecture, and the Frey-Mazur conjecture. We use anabelian techniques to prove these function field analogues, including some results which are new for Riemann surfaces.

Holding the p-adics in the palm of your hand (with thanks to Matt Kukla)

A few years ago I made a picture of the 3-adic numbers in answer to a MathOverflow question (using the free 3d modeling and rendering software Blender, which I highly recommend despite its steep learning curve). Recently I discovered that I lost the original file, so I recreated it, with the following result:

View fullsize

Really this is \(\mathbb{Z}/243\mathbb{Z}\)

After I posted the picture above on Twitter, Matt Kukla, a budding mathematician and student at the University of Maryland, asked for the source file, and today, he’s posted a beautiful 3D print of the 3-adic numbers!

I've managed to 3D print @littmath's model of the 3-adic integers. The final product came out very nicely — a bit of fuzz on the upper prongs, but that should sand off easily.

Technically this is ℤ/243ℤ, but we've got a finite-filament printer... pic.twitter.com/uRatmHNV6U

— Matt Kukla (@n_category) February 12, 2019

EDIT 5/19/2019: If you’d like to try this yourself, here is the original .blend file and here is an exported .obj file.

What I've been thinking about recently

I wrote a MathOverflow answer just now which also happens to be a pretty good summary of some of the open questions I’ve been thinking about recently. Take a look:

How does Frobenius act on the fundamental group of the projective line minus a set of points?

More Tate curves, more problems

I’m giving an expository lecture on the Tate curve and non-archimedean geometry next Tuesday, November 6, as one of the preparatory lectures for Peter Scholze’s Chow Lectures in Leipzig. I thought the problem set for the lectures might be interesting to people, so here it is! Please let me know if you have any comments.